V. DE LA IMAGEN
AL SONIDO
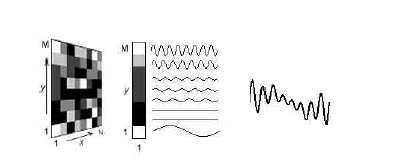
Vamos a generar sonido a partir de una imagen digital en escala de grises en base a las características visuales de la misma. Para ser más precisos, sonificamos una imagen por columnas, creando una onda sonora de cada uno de los píxeles que contiene.
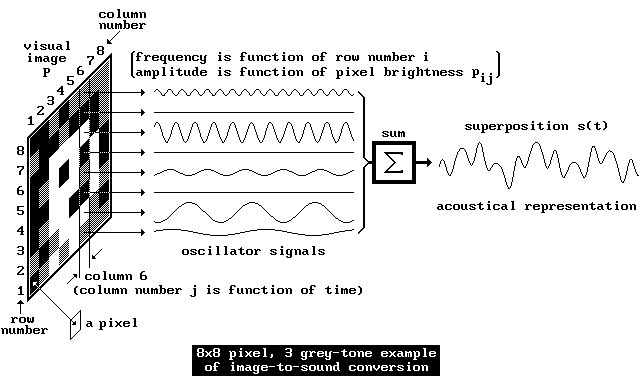
Una intuitiva y estrecha correspondencia entre las características de la imagen y el sonido a producir es el utilizar el nivel de intensidad de cada píxel para dar mayor o menor volumen al sonido generado y utilizar su posición espacial en la dirección vertical para determinar el tono, eligiendo frecuencias mayores para los píxeles a mayor altura en la imagen y viceversa. Para cada columna sumamos las ondas generadas por cada uno de sus píxeles y hacemos un barrido de izquierda a derecha sonificando así todas las columnas y por tanto toda la imagen.

De esta explicación se deduce que el nivel de gris de cada píxel está directamente relacionado con la amplitud de la onda que genera (el volumen del sonido). Asimismo, la altura de cada píxel determina la frecuencia de la onda (que está relacionada íntimamente con el tono del sonido), siendo mayor cuanto más alto se encuentra en la columna. La función sinusoidal utilizada para la generación de la onda correspondiente a la sonificación de cada píxel viene dada por la Ecuación:
![]()
siendo O el valor de la onda en cada instante t, A su amplitud, dependiente del nivel de intensidad del píxel en la columna, I(y), y w su frecuencia., dependiente de la altura del píxel en la columna y. Por poner un ejemplo, en la figura de arriba se observa que la onda correspondiente al píxel blanco de la fila más baja tiene la misma amplitud que su homóloga de la fila superior, sin embargo ambas difieren en su frecuencia. La suma que se forma de la contribución de cada uno de los píxeles es el sonido correspondiente a la primera columna. Para sonificar la imagen entera, barremos las sucesivas columnas, generando así el sonido total compuesto por los sonidos individuales de cada una de ellas. La contribución a la onda de la columna de los dos píxeles blancos del sencillo ejemplo viene expresado por las ecuaciones:
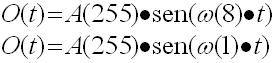
siendo 255 el nivel de gris correspondiente al color blanco y 1 y 8 las alturas respectivas de ambos píxeles. También es interesante observar en la misma figura que los píxeles negros generan ondas de amplitud igual a cero, sean cuales sean sus alturas, y por tanto sus frecuencias.
La función resultante para una columna x de la imagen se expresa a través de la suma de las contribuciones de cada uno de los píxeles que contiene, llegando así a la ecuación:
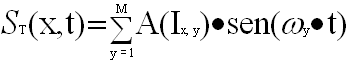
siendo x=1..N, la posición de la columna en la imagen de dimensiones MxN, y=1..M la posición del píxel en la columna, Ix,y el nivel de gris del píxel situado en la posición (x, y) de la imagen, y wy la frecuencia perteneciente a la altura y.
La adhesión sucesiva de todas las funciones suma correspondientes a las columnas formará finalmente el sonido total de la imagen.
De esta manera, la duración del sonido debido a la sonificación de toda la imagen será suma de las duraciones parciales de las ondas de todas las columnas. Si llamamos a ese tiempo T. La duración del sonido de cada columna será T/N.
Cuando la imagen k-1-ésima ha sido transformada en sonido, la imagen k-ésima es muestreada, digitalizada y almacenada como N columnas x M filas en lo que se llama la matriz de píxel P(k).
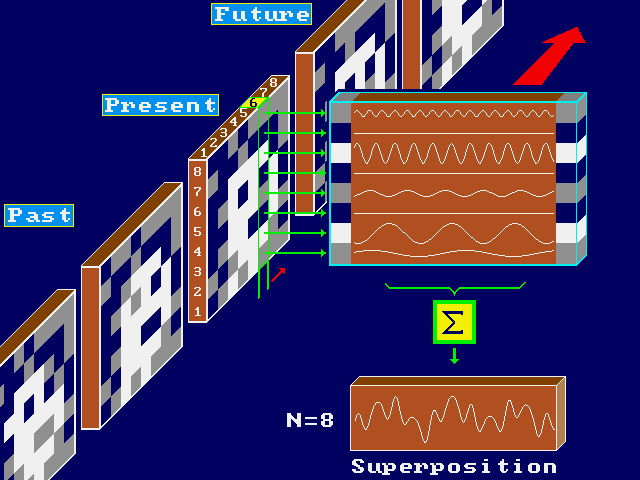
Los valores de cada elemento de la matriz de pixel pij(k) es función del número de tonos grises.
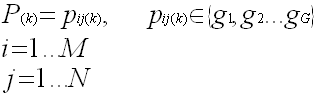
En este proceso de muestreo , digitalización y almacenamiento de la imagen se emplea un tiempo t.
Aquí vemos un ejemplo con M=8, N=8 y G=3. Es decir 8-filas, 8-columnas y 3 tonos grises.
Es fácil darse cuenta de que el acoplamiento de las funciones correspondientes a las columnas para crear la sonificación de toda la imagen creará sonidos extremadamente complejos y sin aparente sentido. Esta supuesta complejidad se incrementa notablemente con imágenes grandes, compuestas por multitud de niveles de gris y con detalles finos. De aquí se deduce la alta necesidad de preprocesar la imagen original y simplificarla en base a las características generadoras del sonido, es decir, el número de niveles de gris de sus píxeles y el tamaño de la misma mediante el procesamiento de imágenes.
La sonificación ofrece varias posibilidades en cuanto al procesado de imágenes, tales como la detección de bordes, véase el filtro de Sobel, el suavizado de imágenes como el filtro de Gauss o el filtro de la Mediana, reducción de la resolución espacial o Cuantización de los niveles de gris.
El conjunto de frecuencias usado en el proceso de sonificación puede ser en principio arbitrario, pero dos buenos conjuntos de frecuencias vienen dados por la distribución lineal (equidistante) o la exponencial. Otros tipos de distribuciones de frecuencia usadas en el dispositivo son la escala de Mel , la escala de Bark y la escala natural.
El uso de la Escala Natural expresa de un modo más intuitivo la geometría expuesta por los píxeles de la imagen. Una persona tiene el oído culturalmente educado de tal manera que dos notas musicales consecutivas que no guardan la misma distancia en frecuencia que otro par consecutivo, lo interpreta como equidistante. Este hecho es fácilmente demostrable. Definimos un salto unitario como el intervalo entre una nota musical y la siguiente. De ésta forma, a pesar de que los intervalos Mi4-Fa4 y Fa4-Sol4 son de un semitono y un tono respectivamente, según nuestra definición corresponderían ambos a un salto unitario.
Para este ejemplo, las distancias en frecuencia de ambos intervalos son de 20 y 43 Hz, lo que contrasta con las demás escalas de frecuencias utilizadas, principalmente la lineal pues queda patente que la escala natural es definitivamente no lineal. La escala natural se utiliza fundamentalmente para imágenes de dimensiones pequeñas pues tratamos de no utilizar más notas que las que contenga una octava. Sin embargo, otra escala que podemos utilizar es la cromática para la que nuestro salto unitario se corresponde con un semitono. Esta escala es útil para imágenes algo más grandes pues en una única octava tenemos hasta 12 sonidos diferentes.

El sonido creado tras el barrido de la imagen representará a la propia imagen y llevará toda la información que pudiera contener. Por este motivo, y aunque “escuchar” una imagen no sea una tarea sencilla, podemos llegar a entenderla. Esta aproximación al significado de la escena puede tener especial importancia en personas con discapacidades visuales, y en concreto en casos de cegueras parciales o totales.