En este tipo de grabación se hace necesario obtener un conjunto de muestras de la señal, aunque no de la sonora si de una señal eléctrica equivalente. En principio, si estas muestras están lo suficientemente cercanas en el tiempo la reconstrucción de la señal podría ser bastante aceptable.
La obtención de estas muestras es un proceso modelado matemáticamente de forma satisfactoria y es lo que se conoce como muestreo de una señal.
Dada una señal x(t) limitada en banda, es decir que fuera de un intervalo centrado en 0 su Transformada de Fourier es nula:
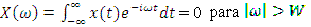
Gráficamente:
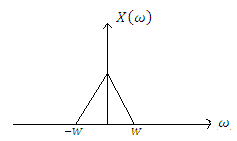
Si se multiplica esta por un tren de impulsos formando una combinación de muestras multiplicadas por deltas, esta nueva señal mediante un filtro adecuado puede generar exactamente la señal original x(t).
La señal obtenida al multiplicar por el tren deltas es la siguiente:
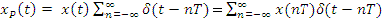
La sucesión de valores ...x(-T),x(0),x(T),x(2T)..., teóricamente infinita contiene la información de la señal original en instantes de tiempo separados T, a este valor se le conoce como periodo de muestreo.
El multiplicar a la señal original x(t) por un tren de impulsos es una forma idealizada de obtener muestras de la señal, en la práctica esto se realiza por ejemplo mediante un interruptor que permita el paso de la señal cada T segundos. Evidentemente en la práctica se trabajará con una sucesión finita de valores, pero el éxito de esta operación se debe a que el modelo matemático presentado anteriormente garantiza la reconstrucción perfecta de la señal.
Se tiene que la transformada de la señal x(t) multiplicada por el tren de deltas es :
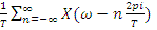
Gráficamente:
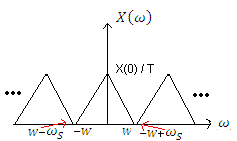
Si se hace pasar esta señal por un sistema LTI con función de transferencia un filtro paso bajo perfecto de amplitud T y que permita el paso de las frecuencias de la señal original, las comprendidas entre -W y W, se recupera exactamente la señal original.
Para ello es necesario que los espectros de las X(w-n2pi/T) no se superpongan, fijándose en la figura anterior se obtiene que una condición necesaria y suficiente es que :
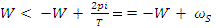
A ws se le conoce como pulsación o frecuencia de muestreo y como se desprende de la inecuación anterior está tiene que ser mayor que el doble de la máxima componente frecuencial de la señal. A la inecuación anterior se le conoce como condición de Nyquist.
Puede parecer que la condición de señal limitada en banda es una restricción bastante grande, pero como ya hemos visto resulta que el espectro audible está comprendido entre 20 Hz y 20KhZ por lo que si la señal que se quiere muestrear tiene componentes frecuenciales situadas por encima de ese umbral, se pueden eliminar sin temor con un filtro paso bajo.
De esta forma :
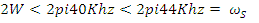
Si no se llega a cumplir este requisito se produce el fénomeno de aliasing, los espectros se superponen y el Teorema de Muestreo no garantiza que se recupere íntegramente la señal.
El modelo anterior es un modelo teórico, no se puede conseguir un filtro paso bajo perfecto, ni un tren de deltas infinito, por la capacidad finita de los ordenadores y por la no existencia física de la "función delta", pero los modelos viables parten de este anterior, y si ni siquiera se cumplen los requisitos en este modelo, el más ideal, más probable es que en la práctica no se obtenga la señal original.
Las muestras obtenidas contienen la amplitud de la señal en el momento que fueron realizadas, para almacenar estos datos en dispositivos electrónicos, para su posterior almacenamiento en soportes de grabación, será necesario transformarlas a números binarios para almacenarlas en registros que usen Flip-Flops por ejemplo o en dispostivos de memoria como RAM o ROM. Evidentemente si la amplitud no es un número entero habrá que redondearla hacia un valor que si lo sea y que tendrá una correspondencia en binario. Este proceso se denomina cuantificación, y como ya se prevé solo por el hecho de redondear se esta cometiendo un error, denominado error de cuantificación que afecta a la calidad sonora final pero se compensa con otros ventajas de usar este tipo de grabación.
La precisión con la que se almacena la muestra depende del número de bits utilizados, se suelen usar entre 16 y 24 bits.
Los procesos anteriores se pueden resumir gráficamente de la siguiente forma:
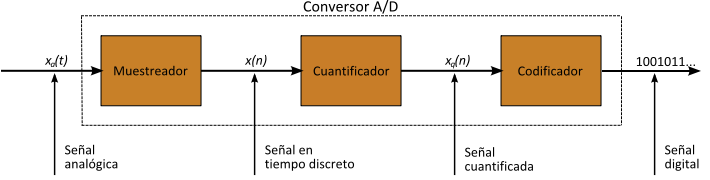
Figura 7. Conversor Analógico Digital. Imagen tomada de [11] |
Una vez que se tiene la información binaria se dispone a almacenarla de diferentes metódos explicados a continuación.