El diseño del Amplificador Operacional consta básicamente de tres estapas, que colocadas en cascada obtienen las características deseadas.
La etapa de entrada o etapa diferencial tiene como objetivo proporcionar una alta ganancia respecto a la diferencia de entradas, y proporcionar una alta resistencia de entrada, pues va a ser la resistencia de entrada del amplificador completo. La resistencia de salida no es tan importante pues con la resistencia de entrada de la segunda etapa se puede realizar un buen ajuste, un circuito equivalente simplificado:
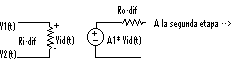
Para llevar a cabo el estudio se separan las señales V1(t) y V2(t) en sus modos diferencial y común, se analiza cada modo por separado y aplicando superposición se obtiene el resultado final. Pero para agilizar el análisis se puede despreciar el modo común pues la ganancia que se obtiene en este modo es inversamente proporcional a la resistencia que se coloque en los emisores de los transistores, y normalmente se suele utilizar una Fuente de Corriente, implementada con transistores que posee una gran resistencia de salida.
Etapa de entrada del amplificador uA741:
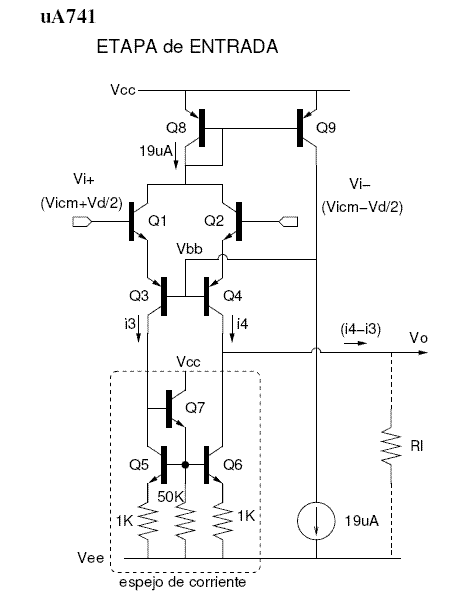
Figura 14. Etapa de entrada del ua741. Imagen tomada de [1] |
Esta etapa esta realizada con transistores NPN por poseer mejores características que los PNP.
En la figura se ha denotado el modo diferencial (Vi+ - Vi-) como Vd y el modo común (Vi+ + Vi- )/2 como Vicm.
En modo diferencial y suponiendo entradas de pequeña amplitud para, gracias al desarrollo de Taylor, obtener el circuito equivalente, se tiene que este es:
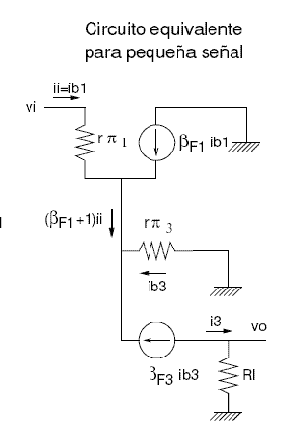
Figura 15. Etapa de entrada en pequeña señal del ua741. Imagen tomada de [1] |
Según [2], se obtiene que Vo/Vi = 1036 y la Resistencia de entrada diferencial de 2.6 MOhm y una resistencia de salida de 5.5 MOhm.
En la etapa intermedia se encuentra el único condensador que no es propio de las capacidades parásitas de los transistores, también llamado condensador de Miller o de compensación. El valor de este condensador es de gran importancia pues va a determinar la frecuencia del primer polo, (obviando los polos introducidos por las capacidades parásitas) y variando su valor se podrá evitar que el Amplificador oscile o se vuelva inestable.
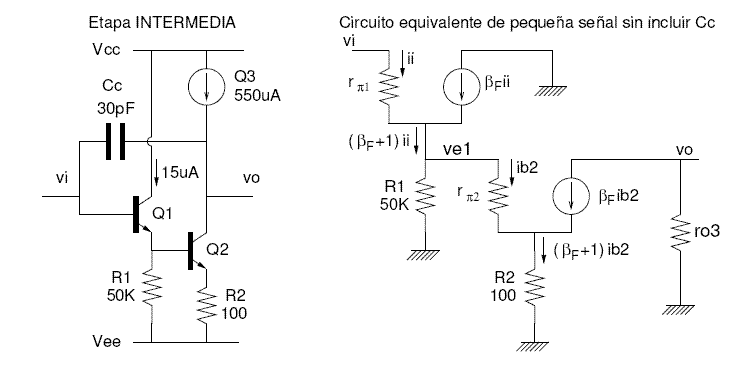
Figura 16. Etapa intermedia del ua741 .Imagen tomada de [1] |
La etapa de intermedia del ua741 es la que se muestra arriba a la izquierda. El condensador de compensación Cc crea una realimentación conectando la salida con la entrada, para eliminar esta realimentación se puede aplicar el teorema de Miller que asegura que si se tiene una etapa donde la entrada y la salida están interconectadas por un condenador y la ganancia del sistema (con el condensador incluido) es menor que 1 un circuito equivalente que se obtiene es el siguiente:
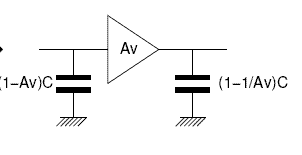
Figura 17. Teorema de Miller .Imagen tomada de [1] |
En la figura superior a la derecha se ha obtenido el circuito equivalente en pequeña señal sin incluir el condensador Cc, seguramente suponiendo que es de valor muy pequeño y por el circulará muy poca corriente:
La ganancia Av=Vo/Vi es -601 que es menor que 1, luego se está en las condiciones de aplicar el teorema. La resistencia de salida de esta etapa es de 94,5 KOhm y la de entrada 5.7 MOhm.
Hasta ahora tenemos las siguientes etapas interconectadas:
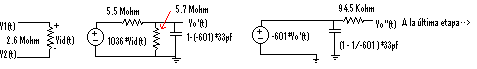
Para calcular mejor la ganancia total en estas dos etapas podemos realizar un equivalente de Thúvenin en bornas de la resistencia de 5.7 Mohm. Desde ahí el voltaje que se "ve" se calcula como un divisor de tensión :
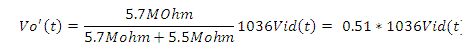
La Resistencia equivalente es el paralelo de 5.5 MOhm y de 5.7 MOhm con un valor de 2.8MOhm. El circuito ahora es el siguiente:
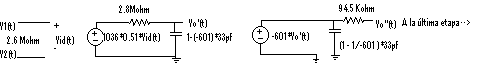
Gracias a esta simplificación Vo'(t) es la salida de un filtro paso bajo RC fácilmente calculable y Vo''(t)=-601*Vo'(t), por lo que la función de transferencia de estas dos etapas se puede calcular como:
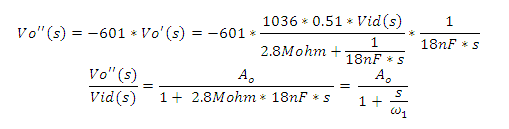
Con
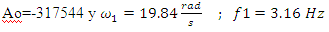
La frecuencia del primer polo es muy baja, simplemente 3.16Hz, pero gracias a la realimentación como se ha comentado, se obtiene una frecuencia muy superior Suponiendo una b de 0.5 : (1+bAo)*3.16Hz = (1+158772)*3.16Hz=502 Khz Aunque falta la etapa final, ya adelantamos que no va a incluir prácticamente ganancia, por lo que la función de transferencia final H(s) es aproximadamente la mencionada anteriormente.
El objetivo de esta última etapa es conseguir una ganancia lo más próxima a la unidad para tener que la función de transferencia final es la calculada anteriormente. Se suele utilizar una configuración en colector común utilizando dos transitores, uno NPN y otro PNP confeccionando una configuración conocida como PUSH PULL. En esta etapa la señal de entrada ya no es lo suficientemente pequeña como para poder hacer un análisis en pequeña señal, y se debe hacer un análisis en gran señal:
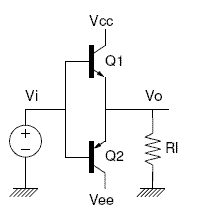
Figura 18. Configuración PUSH PULL.Imagen tomada de [1] |
Con en esta configuración, si la señal Vi es positiva Q2 está en corte y Q1 en la zona activa y por tanto Vo=Vi-Vbe=Vi-0.7, cuando la señal Vi es negativa ocurre lo contrario y Vo= 0.7+ Vi, se observa que el cociente Vo/Vi no es uno, se comete un error de 0.7/Vi. Además si Vi es menor que 0.7, Vo/Vi dista mucho de ser 1.

Figura 19. Ganancia con configuración PUSH PULL. Imagen tomada de [1] |
Una opción para mejorar esto es incluir fuentes de alimentación en las bases de los transistores, de esta forma, cuando Q1 conduce, Vo=Vi+Vbb-0.7 y cuando es Q2 el que lo hace Vo=0.7+Vi-Vbb cometiendo un error de Vbb-0.7 / Vi. Si Vbb es similar a 0.7 el error es despreciable y la ganancia es aproximadamente unitaria.
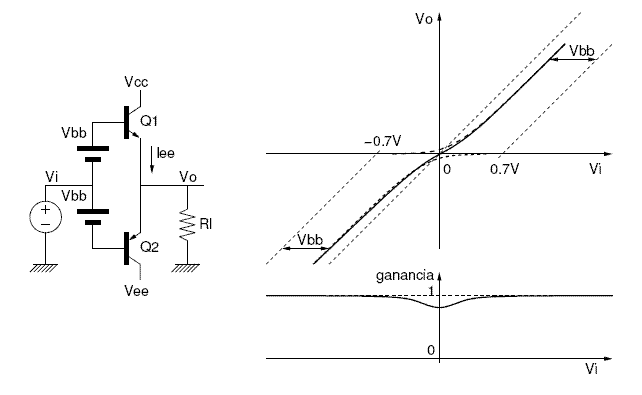
Figura 20. Configuración PUSH PULL con fuentes de alimentación.Imagen tomada de [1] |
Aún así, si Vi es próximo a 0, aun incluyendo las fuentes de alimentación la ganancia no se acerca demasiado a 1. Como Vi es muy pequeño, en el desarrollo de Taylor se pueden despreciar los términos de segundo grado en adelante y se puede utilizar el circuito equivalente en pequeña señal.
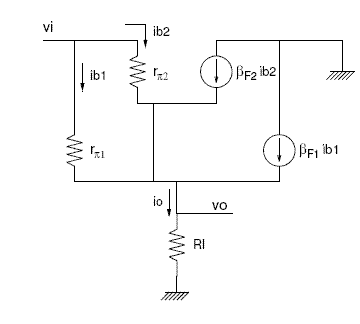
Figura 21. Circuito en pequeña señal. Configuración PUSH PULL con fuentes de alimentación.Imagen tomada de [1] |
Se puede demostrar que Vo/Vi= 2RL/ (2RL + VT/IEE). Para una Rl de 100 OHM, y una IEE de 2.37 mA, se tiene que Vo/Vi es 0.95 y para una IEE de 12.4 mA, Vo/Vi es 0.99. Por lo que para conseguir una función Vo/Vi lo más próxima a 1 habrá que conseguir una gran corriente de Emisor en continua.