 |
Instrumentos de Cuerda |
 |
> Introducción a los
Instrumentos de Cuerda
> Principios de Funcionamiento de
los Instrumentos de Cuerda
> Clasificación de los
Instrumentos de Cuerda
Principios de funcionamiento de los Instrumentos de Cuerda
El mecanismo básico que produce el sonido en todos los instrumentos de cuerda
es el mismo, la única diferencia es que para obtener la vibración, en algunos
casos la cuerda se frota, mientras que en otros se pulsa, o por último se
golpea.
Onda Transversal propagándose a través
de la cuerda
En primera instancia se debe
abandonar la idea de que la cuerda es inextensible. Se tiene una cuerda que en
equilibrio tiene una densidad lineal de masa
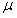 y está bajo la acción de una tensión cuya magnitud es F.
En la siguiente figura A se ilustra un elemento de cuerda dx.
Si se somete la cuerda a pequeñas elongaciones transversales (figura B), la
tensión es prácticamente la misma tensión de equilibrio, de magnitud F.
La sección izquierda del elemento está desplazada en y,
la sección derecha en y + dy . Aquí dy es
la deformación transversal del elemento de cuerda. Sin embargo debe mantenerse
presente que el elemento dx se
deformó en
y está bajo la acción de una tensión cuya magnitud es F.
En la siguiente figura A se ilustra un elemento de cuerda dx.
Si se somete la cuerda a pequeñas elongaciones transversales (figura B), la
tensión es prácticamente la misma tensión de equilibrio, de magnitud F.
La sección izquierda del elemento está desplazada en y,
la sección derecha en y + dy . Aquí dy es
la deformación transversal del elemento de cuerda. Sin embargo debe mantenerse
presente que el elemento dx se
deformó en 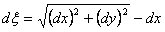 . .

Aplicando la segunda ley de
Newton al elemento de cuerda de longitud dx,
y sabiendo que la aceleración de vibración de su centro de masa es
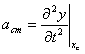 ,
se obtiene, ,
se obtiene,

Las componentes horizontales de
la tensión, 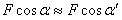 se cancelan y se ha despreciado la fuerza de gravedad, ya que es muy pequeña en
comparación con la tensión. Aplicando la ley de Hooke,
se cancelan y se ha despreciado la fuerza de gravedad, ya que es muy pequeña en
comparación con la tensión. Aplicando la ley de Hooke,

y por tanto se obtiene la ecuación
de ondas,
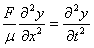
donde las derivadas quedan evaluadas en
x (el centro de masa se acerca al extremo izquierdo del elemento tanto
como queramos).
Como demostraremos a continuación. la solución de esta ecuación de ondas representa una onda que se propaga a
través de la cuerda con una velocidad V:
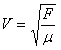
F
se
mide en N y
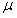 se mide en Kg.m-1 se mide en Kg.m-1
Con esta expresión
se calcula la velocidad de propagación de las ondas transversales en una cuerda
para pequeñas elongaciones. Esta deducción coincide con lo obtenido en la
ecuación diferencial de onda generalizada ya que para la cuerda
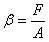 .
.
Solución general de la ecuación
de ondas
La solución general de la ecuación de ondas es de la forma (en lugar de
llamar V, hemos llamado 'c' a la velocidad de propagación):
y = f(c∙t - x)
+ g(c∙t + x)
donde f(c∙t - x) y g(c∙t + x) son funciones arbitrarias cuyos argumentos son (c∙t
- x) y (c∙t + x).
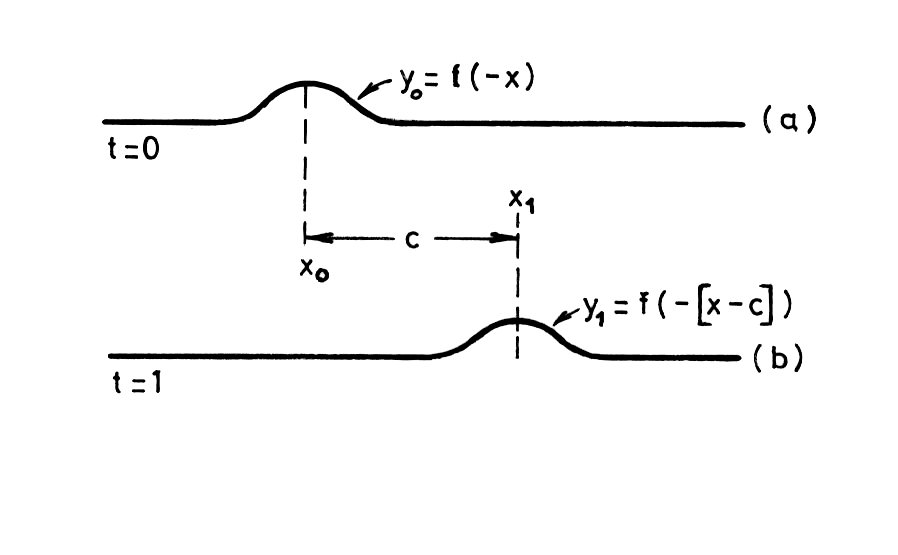
Si dibujamos la función f(c∙t - x) en el instante t = 0, obtenemos la curva yo
= f (-x), que podemos suponer tiene la forma de la siguiente figura (a). En un instante de tiempo tal que t = 1, la curva que
representa será:
y = f(c - x) = f [-(x-c)]
Se observa en la
figura b, a la función para t = 1, que es idéntica a la función para t =
0, excepto que cada valor particular del desplazamiento y, se
presenta en x - c, y en x, por ejemplo, el desplazamiento y1
en x1 es el mismo que yo en xo si x1
- c = xo. Si escribimos esta igualdad de la forma x1 = xo
+ c, se demuestra que la curva tiene un cambio a una distancia c a la derecha
después de un tiempo de un segundo. Por tanto, y = f(c∙t-x) representa una onda
que se mueve hacia la derecha, en la dirección de las X positivas con la
velocidad c. Análogamente se puede demostrar que y = g(c∙t + x)
representa una onda que se mueve hacia la izquierda con velocidad c.
Debemos recordar que la forma de la onda correspondiente para cada una de las
dos funciones arbitrarias permanece constante a lo largo de la cuerda. Esta
conclusión no es completamente cierta en la práctica, ya que hemos hecho unas
suposiciones para encontrar la ecuación de ondas que no se cumplen estrictamente
en las cuerdas reales, ya que estas tienen espesor y existen fuerzas disipativas, lo
que originará que las ondas que se propaguen presenten distorsión. Para cuerdas
relativamente flexibles y con pequeño amortiguamiento, como en los instrumentos
musicales, la distorsión es pequeña si la amplitud de las perturbaciones es
también reducida; pero para amplitudes grandes el cambio de la forma de la onda
puede ser
pronunciado.
Condiciones iniciales y de
frontera
En la práctica, las funciones f(c∙t - x) y g(c∙t + x) no son completamente
arbitrarias, están limitadas por varios tipos de condiciones iniciales y
frontera. Para las vibraciones libres de las cuerdas, la forma matemática para
las condiciones iniciales es que, por ejemplo, los valores para t = 0 están
determinados por el tipo y punto de aplicación de la fuerza de excitación que se
aplica a la cuerda. En los instrumentos musicales las cuerdas pueden entrar en
vibración principalmente por tres procedimientos, en primer lugar,
pulsándolas como en el arpa, guitarra, laúd, etc.; en segundo lugar
golpeándolas como en el piano, y en tercer lugar pueden ser friccionadas como
en el violín, contrabajo, etc.
Además, estas funciones están limitadas por las condiciones frontera en los
extremos de la cuerda. Las cuerdas reales tienen una longitud finita y están
fijas de alguna forma en sus extremos. Si, por ejemplo, los soportes de la
cuerda son rígidos, lo que es cierto para casi todas las cuerdas, la suma de las
funciones f + g tiene un valor nulo en cualquier instante para los puntos
extremos de la misma. El efecto más importante de este tipo de condición
frontera es la necesidad de que el movimiento de la vibración libre de la cuerda
sea periódico.
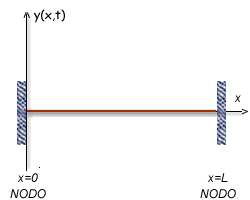
Ondas estacionarias en una cuerda
con extremos fijos
A continuación
se
ilustra una cuerda atada en sus extremos (como una cuerda de guitarra). En este
caso se dice que las fronteras de la cuerda son dos nodos.
Cuando se perturba la cuerda, por ejemplo en su extremo
izquierdo, se genera una onda que se denomina la onda incidente,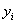 ,
la cual al reflejarse en el extremo derecho origina una segunda onda que se
denomina reflejada, ,
la cual al reflejarse en el extremo derecho origina una segunda onda que se
denomina reflejada, 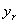 ,
que tiene la misma frecuencia y longitud de onda, ,
que tiene la misma frecuencia y longitud de onda,
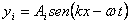 ,
, 
Por
lo tanto, la cuerda oscilará con una superposición de estas dos ondas:

Las condiciones de frontera son:
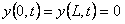
Aplicando la primera condición,
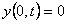 , ,

es decir,
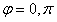 (valores más representativos). Si se toma el valor de
(valores más representativos). Si se toma el valor de
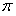 ,
se obtiene, ,
se obtiene, 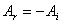 ,
lo cual no es posible puesto que ambas amplitudes deben ser positivas
(amplitudes negativas no tienen interpretación física). Por lo tanto ,
lo cual no es posible puesto que ambas amplitudes deben ser positivas
(amplitudes negativas no tienen interpretación física). Por lo tanto
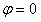 y y
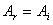 ,
es decir, ,
es decir,
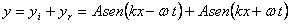
es importante
anotar que 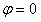 corresponde
a una diferencia de fase entre la onda incidente corresponde
a una diferencia de fase entre la onda incidente
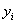 y
la reflejada y
la reflejada
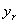 en
x=0 de en
x=0 de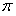 , ,



En definitiva, la cuerda oscila con
una superposición de dos ondas viajeras propagándose en sentidos opuestos pero
con todos sus parámetros iguales (amplitud, número de onda, longitud de onda,
frecuencia, período).

A continuación se ilustra este hecho, representando en color
negro la onda total:

Como
ya hemos visto, a este tipo de ondas se les denomina ondas estacionarias.
Nodos y Vientres:
En una onda estacionaria hay elementos
del medio cuyos centros de masa se mantienen quietos en todo instante (nodos) y
hay elementos del mismo cuyo centro de masa vibra en una posición denominada
vientre en donde la pendiente es cero en todo instante de tiempo. Entre nodo y
nodo o entre vientre y vientre consecutivos hay una separación de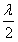 por lo que la separación entre vientres y nodos consecutivos será
por lo que la separación entre vientres y nodos consecutivos será
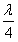 . .
Para mostrar lo dicho en el párrafo
anterior, se debe tener en cuenta que en los nodos se deben cumplir que la
velocidad de vibración en todo instante es nula ( )
y en los vientres la pendiente de )
y en los vientres la pendiente de
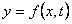 debe ser nula en todo instante (
debe ser nula en todo instante (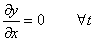 )
. )
.
Posición de los nodos:


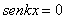

sin embargo, para el caso de la cuerda que se está
considerando, n = 0,1,2,3,.., ya que no tendrían
sentido los valores negativos.
Adicionalmente, la separación entre dos nodos
consecutivos será,
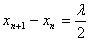 ,
es decir, ,
es decir,
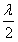 . .
Posición de los vientres:
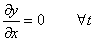


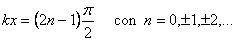
para el caso de la cuerda que ese está
considerando, n= 1,2,3,...
Análogamente al caso de los nodos, se puede
mostrar que la separación entre vientres consecutivos es igual a
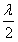 . .
Aplicando la segunda condición de frontera
a la ecuación,
 , ,



aquí se
deben desechar los valores negativos de n
ya que corresponderían a números de onda k negativos
y por ende como 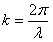 ,
a longitudes de onda negativas, lo que no tendría significado físico. También se
debe desechar ,
a longitudes de onda negativas, lo que no tendría significado físico. También se
debe desechar 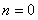 ,
puesto que correspondería a una longitud de onda infinita, lo que significaría
que el medio no vibra (caso trivial en el que la cuerda no vibra). En definitiva
se obtiene, ,
puesto que correspondería a una longitud de onda infinita, lo que significaría
que el medio no vibra (caso trivial en el que la cuerda no vibra). En definitiva
se obtiene,
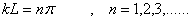 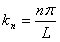
como
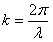 y
y 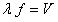 ,
se pueden escribir también relaciones equivalentes para las longitudes de onda y
para las frecuencias, ,
se pueden escribir también relaciones equivalentes para las longitudes de onda y
para las frecuencias,

De estas dos
relaciones se concluye que:
-
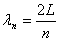 significa
que la cuerda sujeta por sus extremos vibra
formando una onda estacionaria, y en la longitud de la cuerda caben
exactamente un número entero de semilongitudes de onda: significa
que la cuerda sujeta por sus extremos vibra
formando una onda estacionaria, y en la longitud de la cuerda caben
exactamente un número entero de semilongitudes de onda:
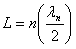 . .
-
La cuerda tiene una
colección de frecuencias a las cuales podrá vibrar como onda estacionaria. A
estas frecuencias se les denomina frecuencias
propias o frecuencias naturales
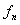 .
A la frecuencia más baja, .
A la frecuencia más baja,  se
le denomina frecuencia del primer armónico
o frecuencia fundamental. A la segunda frecuencia se
le denomina frecuencia del primer armónico
o frecuencia fundamental. A la segunda frecuencia
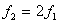 ,
se le denomina frecuencia del segundo armónico,
y así sucesivamente. ,
se le denomina frecuencia del segundo armónico,
y así sucesivamente.
-
A cada armónico n
( o también llamado onda estacionaria n)
de la cuerda con extremos fijos, le corresponde
una onda dada por la ecuación :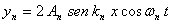 . Y a la expresión
. Y a la expresión 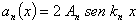 se
le denomina perfil del armónico. se
le denomina perfil del armónico.
-
Como
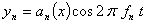 ,
se concluye que cuando la cuerda con extremos fijos
vibra como una onda estacionaria (es decir, en
un armónico), todas sus elementos (exceptuando
los nodos) vibran con movimiento armónico simple pero con una amplitud que
dependerá de la posición del elemento sobre la cuerda, ,
se concluye que cuando la cuerda con extremos fijos
vibra como una onda estacionaria (es decir, en
un armónico), todas sus elementos (exceptuando
los nodos) vibran con movimiento armónico simple pero con una amplitud que
dependerá de la posición del elemento sobre la cuerda,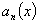 ,
pero todos tienen igual frecuencia ,
pero todos tienen igual frecuencia
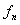 . .
- Cada armónico tiene una
longitud de onda
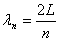 y
una frecuencia y
una frecuencia
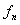 diferentes
a los demás armónicos. Sin embargo, el producto de estas dos magnitudes debe
ser constante para todos los armónicos, diferentes
a los demás armónicos. Sin embargo, el producto de estas dos magnitudes debe
ser constante para todos los armónicos,

A
continuación se analizarán los primeros armónicos de esta
cuerda sujeta por sus extremos.
En la figura, N significa nodo (elementos de la
cuerda que no vibran) y V vientre (elementos de la
cuerda que vibran con la máxima amplitud
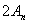 ).
La relación de la columna 3 se obtiene observando las gráficas de la columna 2.
La relación de frecuencia de la columna 4 se puede obtener a partir de la
columna 3 sabiendo que ).
La relación de la columna 3 se obtiene observando las gráficas de la columna 2.
La relación de frecuencia de la columna 4 se puede obtener a partir de la
columna 3 sabiendo que
 . .
|
Nº ARMóNICO
|
PERFIL DEL ARMóNICO
|
LONGITUDES DE ONDA CONTENIDAS EN L
|
FRECUENCIA
|
|
1
|
|
|
 |
|
2
|
|
|
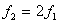 |
|
3
|
|
|
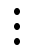 |
|
|
|
|
|
|
n
|
|
|
|
Mediante
la observación de los perfiles de los armónicos se puede concluir que:

donde n
son los números naturales, V la velocidad de propagación de las ondas
viajeras transversales en la cuerda y L la longitud de la cuerda.
Resumiendo, si partimos de una cuerda tensa y elástica de longitud L
sujeta por sus dos extremos (condición necesaria para que entre en vibración) y producimos una
perturbación en su centro desplazándola de su posición de equilibrio, ésta
tenderá a recuperar la posición de equilibrio mediante oscilaciones que
perturbarán el aire generando ondas sonoras. Puesta en movimiento vibratorio una cuerda musical, las vibraciones se
propagan a lo largo de la misma reflejándose en sus extremos, formando puntos
donde la amplitud de las vibraciones es nula (nodos), mientras que se alcanzan
otros puntos donde la amplitud de las vibraciones es máxima (vientres).

Las
frecuencias de oscilación de la cuerda, son equivalentes a las frecuencias de
las ondas producidas en el aire al perturbarse por el movimiento de las
cuerdas, produciendo un sonido. El valor de las frecuencias producidas por una
cuerda de longitud L, es (l = v/f):
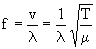
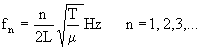
donde T es la tensión a la que está sometida la cuerda, anteriormente
llamada F, y
m = S·
r es la masa por unidad de longitud, siendo S el área de la sección de la
cuerda y m su densidad lineal.
A partir de la ecuación anterior se pueden extraer varias conclusiones: se
observa que si se varía la tensión T de la cuerda, manteniendo su longitud y su
masa constante, se obtienen sucesivas series de armónicos, de forma análoga se
obtienen manteniendo fija su tensión y su masa y variando su longitud. Así mismo, si se aumenta la tensión
o se disminuye su longitud, la frecuencia aumenta. De forma análoga, para igualdad de
longitud y tensión en la cuerda, las pesadas y gruesas producen sonidos más
graves que las ligeras y delgadas.
Vibraciones producidas por la pulsación
de una cuerda fija
Cuando una cuerda fija por sus dos extremos es puesta en
vibración mediante la pulsación de la misma, ésta adquiere lo hace a partir de
varios de sus modos de resonancia naturales al
 mismo tiempo. mismo tiempo.
Las frecuencias de resonancia con las que vibrará dependerán
del desplazamiento inicial provocado por la pulsación.
La animación de la izquierda ilustra la vibración de una
cuerda pulsada a 1/3 de su longitud. Se pueden observar dos pulsos de onda
desplazándose, uno en el sentido de la agujas del reloj, y el otro en el
contrario. El tiempo de una propagación completa es un periodo. Si la cuerda
vibra con una frecuencia fundamental de 440 Hz, este ciclo de vibración se
repetirá 440 veces por segundo.
Por el Teorema de Fourier, podemos descomponer la vibración
de la cuerda en sus diferentes armónicos.
El dibujo de abajo muestra la descomposición en los 6
primeros armónicos de la posición inicial de la cuerda al ser pulsada a 1/3 de
su longitud.
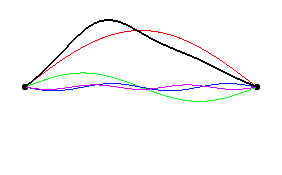
Como se puede ver, están presentes los siguientes armónicos:
n=1,
n=2,
n=4, n=5
Los armónicos n=3 y n=6 no están presentes.
Esto es debido a que los patrones de onda estacionaria poseen un nodo en el
lugar donde se ha realizado la pulsación. De este modo, todos los modos de
vibración múltiplos del tercero poseen un nodo en L/3 y no serán excitados.
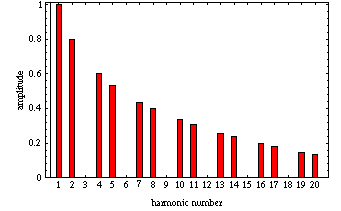 Se
puede construir un "espectro de frecuencias" para la vibración de la cuerda
pulsada del ejemplo determinando la amplitud de todos los modos presentes en la
vibración. Se
puede construir un "espectro de frecuencias" para la vibración de la cuerda
pulsada del ejemplo determinando la amplitud de todos los modos presentes en la
vibración.
La figura de la izquierda muestra este espectro para el ejemplo de la cuerda
pulsada a 1/3 de su longitud. Notar que, como se ha explicado, todos los modos
múltiplos de 3 no están presentes.
Modos de resonancia de
la caja de un violín
El factor determinante a la hora de determinar el timbre de un instrumento de
cuerda es, sin duda, el modo de resonar de la caja de resonancia, es decir, el
modo en que atenuará o amplificará los armónicos generados por las cuerdas al
ser excitadas.
A continuación podemos ver los modos de resonancia de una caja de violín,
obtenidos mediante el Método de Chladni.









|




![]() [Introducción] [El
Sonido] [Las
Escalas Musicales]
[Los Instrumentos
Musicales] [Cuerda]
[Viento]
[Percusión]
[Introducción] [El
Sonido] [Las
Escalas Musicales]
[Los Instrumentos
Musicales] [Cuerda]
[Viento]
[Percusión]