Simetría y recursividad

Un procedimiento básico para obtener cohesión en una pieza de música es la reafirmación de una secuencia de sonidos una y otra vez, de una forma variada, para evitar la monotonía y dar carácter a la composición.

Algunas de las técnicas usadas para dar unidad a una composición, están basadas en el plano geométrico ya que las transformaciones musicales están íntimamente relacionadas con las transformaciones geométricas básicas. Transformaciones geométricas como la rotación, la traslación y la reflexión las encontramos en la mayoría de las melodías populares y el análisis de las obras maestras musicales nos llevará a encontrarlas.

Así, una frase musical tendrá motivos que se repiten en forma idéntica o se repiten en forma más aguda o más grave; en otras ocasiones, en vez de subir, bajan o retroceden. Este es un recurso muy utilizado, aunque normalmente no lo asociamos con las Matemáticas.

 

Aritmética modular

Una de las cosas más necesarias para que la música "funcione" es que tenga unidad. Es claro que una cantidad de sonidos que se relacionen entre sí sin nada que los relacione (digamos las esquilas de un hato de ovejas, superpuestas al murmullo de un rio, mientras pasa un helicóptero y al lado otro excursionista tiene la radio demasiado alta), va a ser difícil de percibir como experiencia musical unitaria, aunque puede admitirse que haya quien disfrute de tal experiencia sonora.

Necesitamos más bien algo que nos haga pensar que la obra se relaciona consigo misma, que cada momento que oímos, se relaciona con los que hemos oído o los que nos quedan por oír —las formas en que se puede conseguir esto son incontables, y no excluyen el contraste—.

Dentro de las formas más primitivas —que está lejos de significar toscas— de conseguir esto, tenemos la repetición de una línea melódica no demasiado larga. Esta repetición aportará unidad a la obra, logrando que nuestro oído alcance satisfacción. Esta práctica es el origen, por ejemplo, de todas las formas musicales basadas en el ostinato.

Lo malo de este procedimiento es que puede, fácilmente, producir demasiada unidad, y acabar resultando aburrido.

Otra de las posibilidades para crear unidad es limitar el rango de frecuencias con que trabajamos: en lugar de emplear todo el espectro de frecuencias comprendido entre los 40 y los 20.000 Htz que abarca el oído humano, limitamos estas frecuencias a unas pocas. Así, elegimos unas pocas frecuencias con las que trabajar, y formamos escalas.

El intervalo de octava, por motivos en parte físicos (es singularmente presente en la naturaleza) y en parte biológicos (el registro de mujeres y hombres cuando cantan juntos difiere normalmente en esa cantidad), acaba dominando la elección de esas frecuencias, de forma que lo usual en todas las culturas es que dentro de una octava se elijan ciertas frecuencias y se repitan en todas las demás. Los pocos casos en que eso no ha sido exacto es cuando se ha dispuesto de instrumentos —las steel drums tropicales, por ejemplo—, cuyo rendimiento difiere en cada octava.

Con esto se llega a que las escalas se han tratado de una forma que, a partir de ahora, denominaremos modular. Si observamos un reloj, no nos parece ilógico que después de las doce venga la una. O a quien juegue a las cartas, tampoco le parecerá extraño que en la baraja francesa después de la reina y el rey vengan el as y el dos. Son casos, por así decirlo, en que imponemos un orden pero no un principio y un fin.

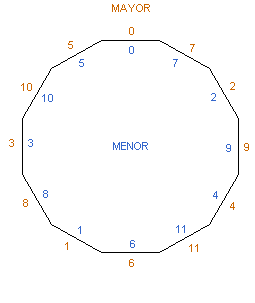
Observemos una escala diatónica normal.

       

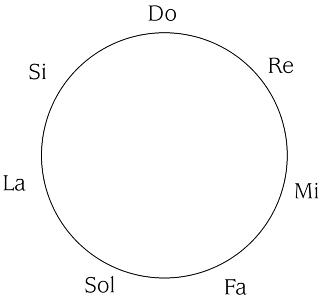
Podemos observar que se ha optado por representarla en círculo. A todos nos han hecho en el colegio aprender "do, re mi, fa, sol, la, si, DO". Por tanto es sensato adoptar una disposición circular que represente esta modularidad.

Aquí podemos observar lo mismo con una escala cromática.

                

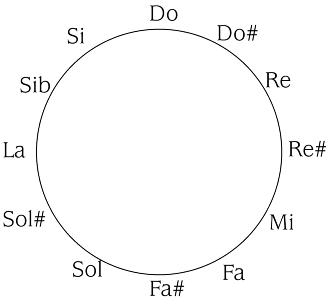
Volvamos ahora a cómo usar repeticiones y aportar además de unidad, variedad. Para nuestro ejemplo, digamos que el fragmento melódico que deseamos repetir es DO- RE- MI- SOL, que represento a continuación como una figura geométrica dentro de la escala diatónica.

                

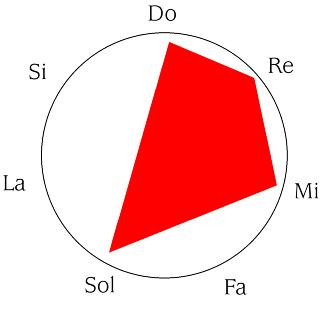
Una primera posibilidad consistiría en lo que llamamos transportar, que consistiría en repetir las mismas distancias desde una nota diferente, si comenzamos desde RE, que es la siguiente a DO, tenemos que:

• La siguiente a RE, es MI
  
• La siguiente a MI, es FA
  
• La siguiente a SOL, es LA

De forma que nuestro D0-RE-MI-SOL, se transforma en RE- MI- FA- LA. El oído se sorprende ante lo nuevo, reconoce el parentesco y queda satisfecho, lo que es una suerte porque es un procedimiento de construcción melódica que ha marcado la inmensa mayoría de la música, de, por ejemplo, Bach —un caso diáfano es la invención número 1— o Mozart.

Es una operación equivalente a un giro, si seguimos con nuestra analogía visual.

                 

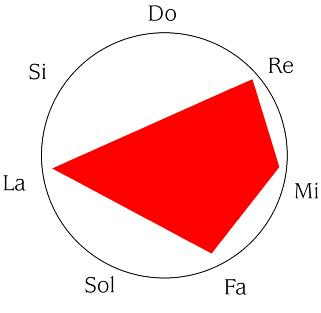
Otra forma en que podríamos haber hecho esto es numerando las notas:

• Do=0
• Re=1
• Mi=2
• Fa=3
• Sol=4
• La=5
• Si=6

Con lo que nuestro DO- RE- MI- SOL, se convierte en [0, 1, 2, 4].

Puesto que la diferencia entre 0 y 1 (do y re, a donde queremos transportar el fragmento) es uno, no tenemos más que añadir 1 a cada miembro de esta hilera de números para conseguir [1, 2, 3, 5], que al retraducir, nos da RE- MI- SOL- LA. Los músicos quizá puedan pensar que es más difícil hacerlo así, pero es un procedimiento que conviene conocer.

Es obvio que para un transporte ascendente debemos sumar, y para uno desdendente, restar.

Hay sin embargo, un problema con este procedimiento. Supongamos que quiero transportar el fragmento a FA. La diferencia entre DO y FA es 3, con lo que [0, 1, 2, 4], se convertiría en [3, 4, 5, 7]. Y resulta que 7 no lo tenemos definido en la tabla anterior.

La solución es restar 7 (el número de notas de esta escala) de todo número mayor o igual que 7, tantas veces como sea necesario hasta obtener un número entre 0 y 6. De la misma forma, si en algún momento obtuviésemos resultados negativos, habría que sumar 7, hasta conseguir lo mismo.

En otras escalas de un número diferente de notas, los resultados serían distintos en el transporte. En la escala cromática, DO- RE- MI- SOL se convertiría en RE- MI- FA#- LA. En los grafismos,

                 

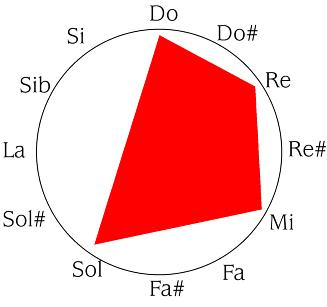
se convertiría en

                   

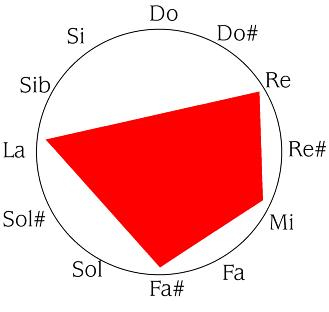
Y, obviamente, en el procedimiento numérico, hay que numerar de 0 a 11, y restar o sumar doces en consecuencia.

 

Técnicas de transformación

Una de las ventajas que nos proporcionaba el transporte era la de provocar simultáneamente unidad y variedad. Es evidente que cualquier técnica de este tipo nos va a resultar extraordinariamente útil, por su economía.

La primera técnica se denomina inversión o movimiento contrario. Consiste en respetar el perfil melódico, pero invertir la dirección del intervalo. Es decir: los saltos melódicos ascendentes los convertimos en descendentes y viceversa.

El ejemplo que veníamos usando era DO- RE- MI- SOL. DO- RE y RE- MI son segundas ascendentes, así contestaremos con segundas descendentes, DO-SI y SI-LA. MI- SOL es una tercera ascendente, así que contestaremos con una tercera descendente desde LA, LA- FA, así que la inversión será DO- SI- LA- FA

Dentro de nuestra analogía gráfica, significa que

                

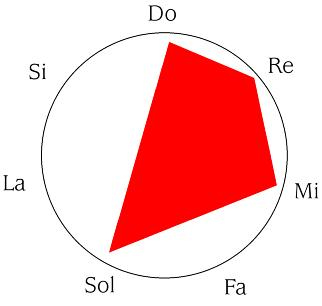
se convierte en

                 

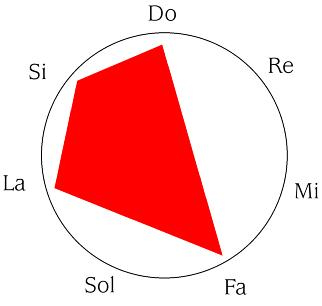
que, como podemos observar, es claramente la figura simétrica al original.

Numéricamente, expresábamos DO- RE- MI- SOL como [0, 1, 2, 4]. ¿Podemos a partir de estas cifras calcular la inversión?

Sí. Vamos a restar cada uno de estos elementos de 7, que es el número de notas de la escala que hemos elegido emplear.

• 7-0=7
• 7-1=6
• 7-2=5
• 7-4=3

Con lo que nos queda [7, 6, 5, 3].

Volvemos a encontrarnos con que 7 no está definido. Y la solución es la misma que para el transporte: restamos 7 (o el número de notas que tenga la escala) tantas veces como sea necesario hasta encontrarnos con un número entre 0 y 6 (o entre 0 y el número de notas de la escala). Con lo que nos queda [0, 6, 5, 4], o sea, DO- SI- LA- FA.

Lógicamente, podemos combinar la inversión y el transporte, de forma que obtenemos una buena cantidad de versiones del material original, que cumplen simultáneamente el objetivo de proporcionar unidad y variedad.

Hay también que decir que estos procedimientos se aplican empleando el sentido común. Hay materiales que funcionan especialmente bien o especialmente mal al someterlos a la inversión a a cualquier otra de las transformaciones. No hay ni que decir que el compositor empleará los que funcionen bien.

El siguiente procedimiento se denomina retrogradación. Hasta ahora, nos ha sido cómodo ignorar que las notas que hemos elegido tienen un determinado orden. Ahora necesitamos tenerlo en cuenta. En forma de notas, no hay problema: DO- RE- MI- SOL en su orden normal de lectura aporta toda la información.

En forma gráfica, podemos indicar el orden empleando una flecha.

                  

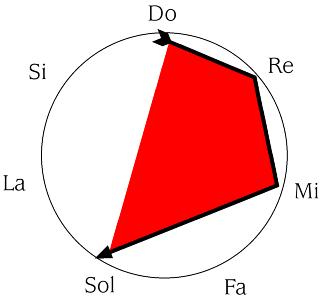
Y en forma numérica, sigue valiendo el orden normal de lectura.

Pues bien, la retrogradación va a consistir en comenzar desde la última nota hasta alcanzar la primera, o, sí se prefiere, en leer de derecha a izquierda las notas.

DO-RE- MI- SOL se convierte en SOL- MI- RE DO.

                    

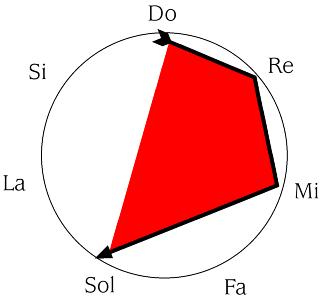
se convierte en

                     

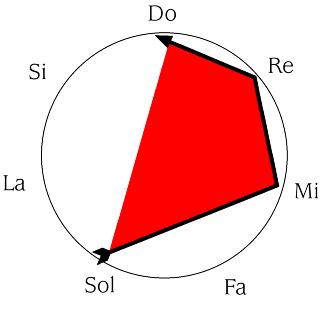
Y [0, 1, 2, 4] se convierte en [4, 2, 1, 0]

La última técnica de transformación temática se denomina inversión retrógrada, y consiste en la aplicación de la inversión y la retrogradación simultáneamente. El orden en que se apliquen es irrelevante, puesto que nos saldrá la misma estructura interválica, aunque transportada, según empecemos por una u otra.

DO- RE- MI- SOL se convierte en FA- LA-SI-DO

En forma gráfica, aplicamos la simetría y cambiamos el orden de lectura.

                 

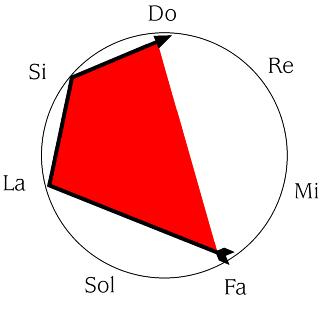
Y, numéricamente, [0, 1, 2, 4], se convierte en [4, 6, 7, 0].

Disponemos entonces, para un material melódico dado, de cuatro versiones:

1. La forma original, que representamos por O.
2. La forma invertida, que representamos con una I.
3. La forma retrograda, que representamos con una R.
4. La forma sometida a inversión retrógrada, que representamos con IR.

Cada una de estas cuatro versiones puede ser sometida a transporte, de forma que disponemos de 28 (7*4, número de notas de la escala multiplicado por el número de versiones) posibilidades de uso. Más, de hecho, si podemos cambiar la escala de referencia.

 

Ejemplos de aritmética modular

La Fuga es un procedimiento de construcción musical o forma musical que se podría definir como una composición polifónica basada en el contrapunto entre varias voces. Su principal característica se basa en su estructura ya que las voces o partes del arreglo reproducen sucesivamente el mismo tema en imitación de las otras en diferentes tonalidades.

Johann Sebastian Bach es el más destacado; llevó la fuga a su apogeo en su obra El arte de la fuga (1749-1750). Durante los siguientes siglos se "redescubrió" la fuga; casos famosos son la Gran Fuga para cuarteto, opus 133 (1825) de Beethoven, y los 24 preludios y fugas opus 87 de Shostakovich.

Johann Sebastian Bach (1685-1750)

El arte de la fuga 2

El arte de la fuga 6

 

El compositor polaco Chopin describió la fuga como “lógica pura”. Era un gran admirador de la obra de Bach y siguiendo sus pasos, aplicó el principio del contraste, alternando los modos mayor y menor, en su obra 24 preludios.

Frederic Chopin (1810-1849)

Aunque teóricamente daría igual qué tonalidad se eligiese (los 12 semitonos son iguales), puede que el pianista, inconscientemente, no toque todos con el mismo ánimo pues la distribución de teclas negras y blancas varía en cada caso.

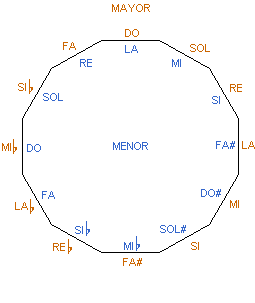
Las tonalidades de estos preludios de Chopin siguen el orden: Do mayor, La menor, Sol mayor, Mi menor, Re mayor, etc. ¿Qué orden es este?

Podemos disponer estas 24 tonalidades en un reloj. La parte externa indica el modo mayor y la interna el modo menor. Así expuesto, se ve claramente que Chopin sigue “el ciclo de quintas”. Es decir, cada nueva tonalidad está 7 semitonos más arriba que la tonalidad anterior del mismo modo. Matemáticamente, esto equivale a sumar 7 en sentido horario.

Repetición y simetrías

La repetición es, probablemente, el procedimiento más usado en música, de hecho, la repetición constante puede causar un efecto hipnótico. También puede provocar una adaptación del oído, como cuando dejamos de percibir el sonido de una lámpara fluorescente.

La repetición no continúa indefinidamente en su manifestación física,  pero nos ofrece una imagen del infinito que en potencia contiene.

Las oberturas de Rossini son un ejemplo de traslación melódica, en dichas obras las frases se repiten, cada vez con más intensidad (crescendo), provocando la expectativa de continuación. El climax se alcanza rompiendo la traslación.

Gioachino Antonio Rossini (1792-1868)

Rossini compuso algunas de las obras más conocidas de todo el repertorio operístico. Una curiosidad de su obra es que recorre las principales ciudades italianas presentando sus óperas, pero en esta época se producen muchos de sus conocidos "pasticcios", o autoplagios que se producían porque tenía que componer numerosas obras cada año y, no estando las ciudades italianas especialmente bien comunicadas, se dedicaba a cortar y pegar trozos completos de óperas anteriores para presentarlas en el siguiente lugar de estreno.

La simetría en música es, sin duda, un caso muy especial. El propio concepto de ritmo a menudo va ligado a la repetición de un determinado sonido o composición, pero donde podemos descubrir curiosas simetrías es en el análisis de las vibraciones emitidas por los diferentes instrumentos. Unas simetrías en el propio pentagrama en el que se ha creado una composición pueden conducir a curiosos efectos auditivos.

Existen interesantes ejemplos en la música clásica: Bach ("Preludio"), Scarlatti ("Sonata en G mayor"), Schumann ("Lotosblume"), Wagner ("Die Meiestersinger")... En la mayoría de estos casos encontramos distribuciones de las notas generadas por traslación o simetría bilateral o giros de media vuelta.

¿Qué pasaría si invirtiéramos toda una partitura?. En general resultaría una composición absurda. Pero hay casos en los que la nueva melodía invertida sí que se puede interpretar. Un bello ejemplo es el "Scherzo-Duetto" de Mozart para dos violines: la obra la pueden interpretar a la vez dos violinistas, cada uno de los cuales lee la partitura en un sentido diferente.

A continuación podemos apreciar dos claros ejemplos de obras maestras que se basan en la repeticióny en la simetría:

 

El bolero de Ravel

 

Quinta sinfonía de Beethoven