 |
Instrumentos de Percusión |
 |
> Introducción a los
Instrumentos de Percusión
> Principios de Funcionamiento de
los Instrumentos de Percusión
> Clasificación de
los Instrumentos de Percusión
Principios de funcionamiento de los
Instrumentos de Percusión
Vibración de barras o varillas
Las varillas que son cuerpos rígidos de notable longitud con relación a sus
restantes dimensiones, sólo necesitan de un punto de apoyo para poder vibrar,
pudiendo hacerlo longitudinalmente, transversalmente, o con vibraciones de
torsión, aunque desde el punto de vista musical, sólo nos interesarán las dos
primeras formas de vibración.
Si la varilla se fija en un extremo y se golpea ligeramente en el otro,
entrará en vibración, sin originarse ninguna flexión secundaria, por lo que sólo
emitirá la frecuencia fundamental sin armónicos y según vaya disminuyendo la
amplitud de la vibración se apagará el sonido. Esta es la base sobre la que se
fundamenta el diapasón, que produce un sonido de frecuencia constante, exento
casi por completo de armónicos. Es por esto que este instrumento se utiliza como
patrón de frecuencias para la afinación de los demás instrumentos.
En todos los instrumentos de varillas, la fuente sonora emite sólo las notas
fundamentales, aunque en forma de onda amortiguada. Esto supone la superposición
de las notas que se van produciendo con la vibración que se amortigua de las
notas anteriores. Esta superposición de sonidos, con frecuencias acordes,
producen un efecto auditivo análogo al de los sonidos armónicos, obteniéndose el
timbre. Como es lógico, también influye la materia de que esté formada la
varilla.
En el caso de las vibraciones longitudinales
a través de las varillas se pueden producir sonidos de un tono definido, siendo la
frecuencia de la vibración inversamente proporcional a su longitud. Si consideramos una barra de longitud L rígidamente fija en sus extremos o
libre en los mismos, las frecuencias de los modos de vibración son:
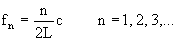
donde c es la velocidad del sonido en la barra, siendo los sobretonos
armónicos.
En cuanto a las vibraciones transversales de las varillas, están regidas por
las leyes opuestas a las anteriores, pues el número de vibraciones del sonido
fundamental producido por una varilla asimétrica que vibra es inversamente
proporcional al cuadrado de su longitud. En el caso de las vibraciones transversales de las varillas simétricas, que es
el tipo de las varillas empleadas en los xilófonos, también influye el número de
vibraciones del sonido fundamental, y varía inversamente al cuadrado de la
longitud de la varilla.
Lo normal es que en este tipo de instrumentos, las varillas estén sujetas por
un extremo, quedando el otro libre. De este modo, las frecuencias de vibración
se obtendrán de la expresión siguiente, que recuerda mucho a la obtenida para
los tubos sonoros cerrados:
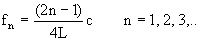
pudiendo comprobar en este caso, que los sobretonos, no guardan una relación
armónica con su fundamental.
Por último, los sonidos fundamentales producidos por una misma varilla, según
vibre simétrica o asimétricamente, son distintos; en el primer caso es más
agudo, manteniéndose en una proporción de 25/4 con relación al segundo.
Por lo tanto, podemos concluir que cuando las varillas vibran
longitudinalmente, lo hacen como los tubos sonoros abiertos, si son simétricas
(sujetas por un sólo punto situado en su centro), y como los tubos sonoros
cerrados, si son asimétricas (sujetos por dos puntos equidistantes del centro y
asimétricos).
Vibración de membranas
La vibración de membranas, se basa en los mismos principios que la vibración
de cuerdas, ya que son materiales elásticos tensados. La diferencia, es que
mientras la cuerda es una línea de puntos vibrando, la membrana es una
superficie, y los puntos nodales de la cuerda se transforman en líneas nodales
en la membrana; por consiguiente las ondas lineales en la cuerda, son de tipo
superficial en la membrana, por lo que las ondas estacionarias son de tipo
bidimensional.
En las membranas ideales vibrantes, los modos de vibración no son armónicos del fundamental,
por lo que no resultarán muy agradables
al oído, presentando varias dificultades para conseguir las diferentes notas,
como es que no se pueden variar sus dimensiones, resultando difícil modificar la
tensión a la que está sometida.
La expresión de
las frecuencias de los modos de vibración de las membranas rectangulares
es la siguiente:
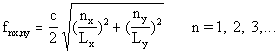
donde c es la velocidad del sonido en la membrana Lx y Ly las longitudes de los
lados de la membrana rectangular.
A continuación se muestran unas
animaciones con algunos de los modos de vibración de una membrana rectangular:
| Modo (1,1) |
Modo (1,2) |
 |
 |
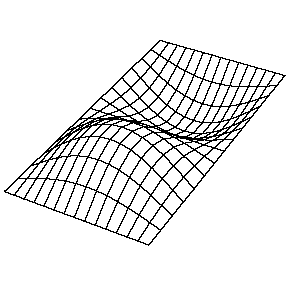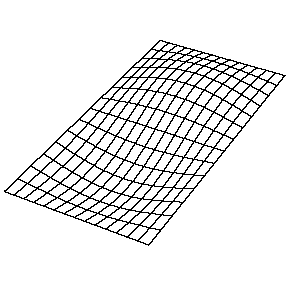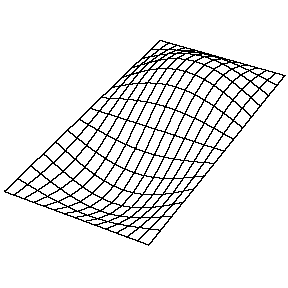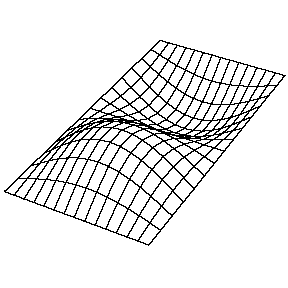| Modo (2,1) |
Modo (2,2) |
 |
 |
La frecuencia fundamental se obtiene al sustituir nx = 1 y ny
= 1, siendo los sobretonos correspondientes a nx = ny
armónicos del fundamental, mientras que para nx = ny no lo
son.
A continuación se muestran algunos de los posibles modos degenerados.
 
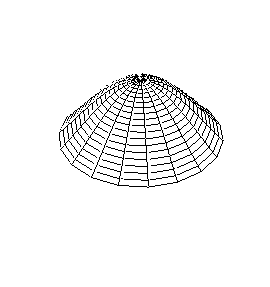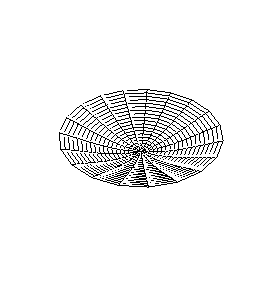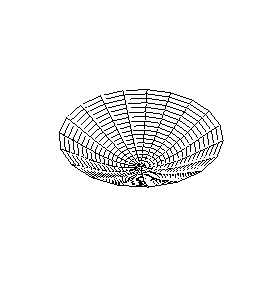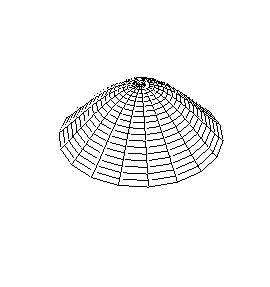
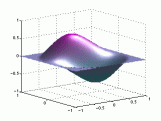
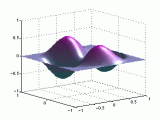
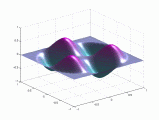
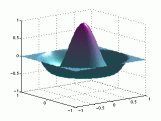
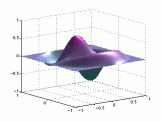
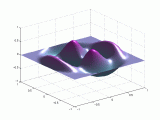
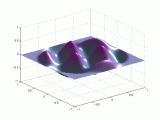
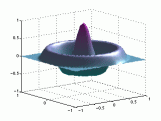
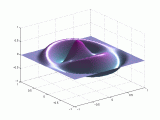
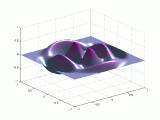
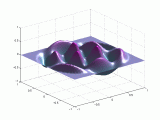
A continuación se representan los modos de vibración transversales de una
membrana circular. Para denominarlos se utiliza una notación compuesta de dos
dígitos: con el primero se indica el número de nodos diametrales y con el
segundo el número de nodos circulares.
| Modo (0,1) |
Modo (1,1) |
Modo (2,1) |
 |
 |
 |
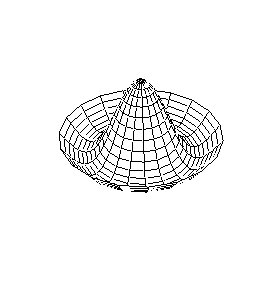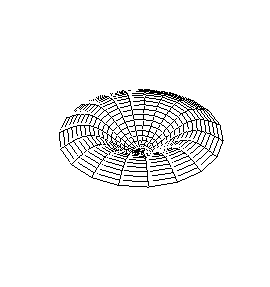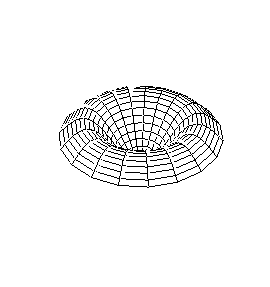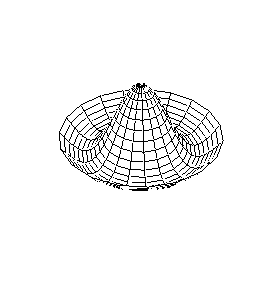
| Modo (0,2) |
Modo (1,2) |
Modo (0,3) |
 |
 |
 |
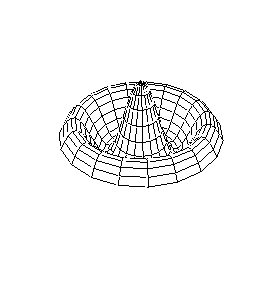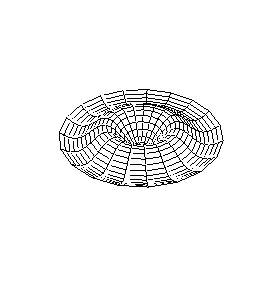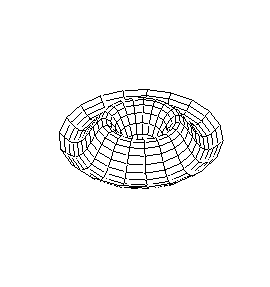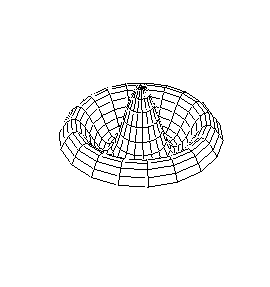En el caso de las vibraciones transversales de las membranas circulares, los sobretonos no son armónicos del fundamental.
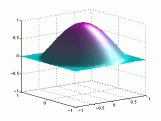
A continuación tenemos otra
representación de dichos modos.
Puedes
pinchar sobre las imágenes para verlas
animadas:
J0
J1
J2
J3
1
2
3
4
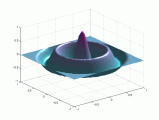
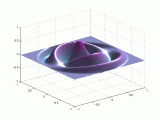
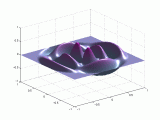
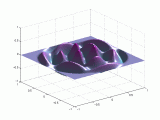
Modos de vibración
transversales de una membrana circular
A continuación se muestran dos imágenes reales de los modos de
vibración de un timbal, la primera obtenida mediante el Método de Chladni y la
segunda mediante interferometría con haces láser:
(Pinchar sobre las imágenes para agrandarlas)
[Fuente: Monográfico sobre Acústica Musical
(Temas 21), Scientific American, Año 2000]
Vibración de placas
La diferencia fundamental entre las vibraciones de una membrana y las de una
placa delgada consiste en que en una membrana la fuerza recuperadora se debe por
completo a la tensión aplicada a la membrana, mientras que en una placa delgada
la fuerza de recuperación se debe por completo a la rigidez de la propia placa y
no a la tensión aplicada en el golpe.
Las placas vibrantes pueden hacerlo transversalmente y dependiendo de la
forma de sujeción, sus modos de vibración son sobretonos que no son armónicos
del fundamental.
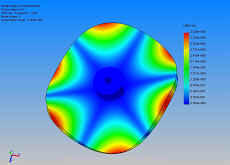
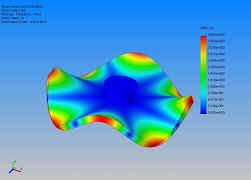
A continuación se muestran algunos modos de vibración de unos
crótalos
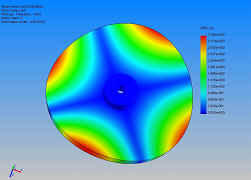
Las vibraciones de campanas podemos aproximarlas a las de placas, siendo
producidas estas al golpearlas con el badajo. Se dan dos tipos de vibraciones:
a) Vibraciones circulares: la
campana conserva su forma de revolución, y sólo cambian los radios de las
secciones perpendiculares al eje de simetría. Desde el punto de vista acústico
tienen escaso interés.
b) Vibraciones radiales: en este
caso, la sección transversal de la campana pierde de temporalmente su forma
circular, para adquirir geometrías ligeramente elípticas. Los modos de vibración
poseen líneas nodales meridianas, debido a la variación periódica de los radios.
Modo
fundamental de vibración de una campana.
En el modo fundamental de vibración, la base de la campana mantiene un
perímetro constante, pero su forma varía (la curva de la base varía entre las
formas extremas V1 v2 V3 v4 y v1
V2 v3 V4, y los puntos N1 N2
N3 y N4 no experimentan desplazamiento en la dirección del
radio) Las curvas trazadas en la campana forman cuatro líneas nodales, que
permanecen en la superficie primitiva de la misma en reposo durante su
vibración, siendo el desplazamiento radial máximo, encontrándose siempre el
punto golpeado por el badajo en la línea nodal.
El sonido producido por una campana depende de sus dimensiones, del espesor
de la parte inferior de la misma, del peso y de su estructura metálica. Influye
también sobre el sonido la forma de suspensión y la posición del centro de
gravedad, así como el peso del badajo.
Una regla empírica utilizada por los fabricantes de campanas es que la
frecuencia de una campana es inversamente proporcional a la raíz cúbica de su
peso. Además, se intenta que los parciales tercero y cuarto formen un acorde
perfecto mayor con el fundamental, y que el quinto sea la octava del
fundamental.
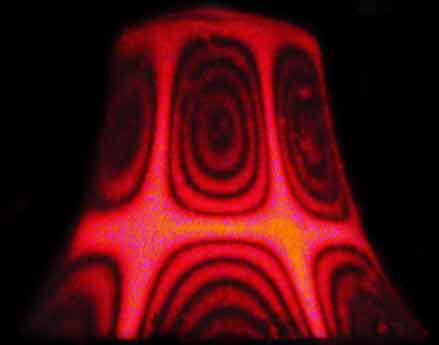
Interferogramas Holográficos
obtenido mediante haces láser, ilustrando
algunos
modos de vibración en una campana.
|
Introducción
|
El Sonido
|
Escalas Musicales
|
Instrumentos
Musicales |
La Orquesta
|
Conclusiones |
Curiosidades
|
Referencias
